Expression Typing

We assume the existence of a function $T$ assigning types to literal constants. It maps integer constants to $\mathsf{Basis}.\mathsf{int}$ , float constants to $\mathsf{Basis}.\mathsf{float}$ , character constants to $\mathsf{Basis}.\mathsf{char}$ , and string constants to $\mathsf{Basis}.\mathsf{string}$ .

We also refer to a function $\mathcal I$ , such that $\mathcal I(\tau)$ ``uses an oracle'' to instantiate all constructor function arguments at the beginning of $\tau$ that are marked implicit; i.e., replace $x_1 ::: \kappa_1 \to \ldots \to x_n ::: \kappa_n \to \tau$ with $[x_1 \mapsto c_1]\ldots[x_n \mapsto c_n]\tau$ , where the $c_i$ s are inferred and $\tau$ does not start like $x ::: \kappa \to \tau'$ .

$$\infer{\Gamma \vdash e : \tau : \tau}{ \Gamma \vdash e : \tau } ... ... \Gamma \vdash \tau' \equiv \tau } \quad \infer{\Gamma \vdash \ell : T(\ell)}{}$$

$$\infer{\Gamma \vdash x : \mathcal I(\tau)}{ x : \tau \in \Gamma ... ...} \; \mathsf{end} & \mathsf{proj}(M, \overline{s}, \mathsf{val} \; X) = \tau }$$

$$\infer{\Gamma \vdash e_1 \; e_2 : \tau_2}{ \Gamma \vdash e_1 : \... ...u_1 \Rightarrow e : \tau_1 \to \tau_2}{ \Gamma, x : \tau_1 \vdash e : \tau_2 }$$

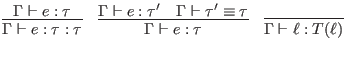
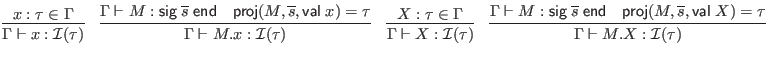
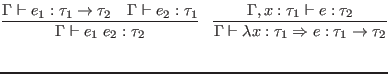
$$\infer{\Gamma \vdash e [c] : [x \mapsto c]\tau}{ \Gamma \vdash e... ...ghtarrow e : x \; ? \; \kappa \to \tau}{ \Gamma, x :: \kappa \vdash e : \tau }$$

$$\infer{\Gamma \vdash e [\kappa] : [X \mapsto \kappa]\tau}{ \Gamm... ...ash X \Longrightarrow e : X \longrightarrow \tau}{ \Gamma, X \vdash e : \tau }$$

$$\infer{\Gamma \vdash \{\overline{c = e}\} : \{\overline{c : \tau}... ...\vdash e_1 : \$c_1 & \Gamma \vdash e_2 : \$c_2 & \Gamma \vdash c_1 \sim c_2 }$$

$$\infer{\Gamma \vdash e \; \texttt{--} \;c : \$c'}{ \Gamma \vdash... ... \texttt{---} \;c : \$c'}{ \Gamma \vdash e : \$(c + \hspace{-.075in} + \;c') }$$

$$\infer{\Gamma \vdash \mathsf{let} \; \overline{ed} \; \mathsf{in}... ...l i: \Gamma \vdash p_i \leadsto \Gamma_i, \tau' & \Gamma_i \vdash e_i : \tau }$$

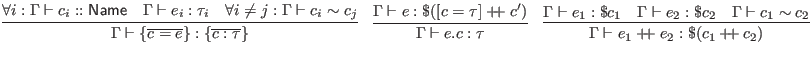
$$\infer{\Gamma \vdash \lambda [c_1 \sim c_2] \Rightarrow e : \lamb... ...amma \vdash e : [c_1 \sim c_2] \Rightarrow \tau & \Gamma \vdash c_1 \sim c_2 }$$