The Ur Standard Library

The built-in parts of the Ur/Web standard library are described by the signature in lib/basis.urs in the distribution. A module $\mathsf{Basis}$ ascribing to that signature is available in the initial environment, and every program is implicitly prefixed by $\mathsf{open} \; \mathsf{Basis}$ .

Additionally, other common functions that are definable within Ur are included in lib/top.urs and lib/top.ur. This $\mathsf{Top}$ module is also opened implicitly.

The idea behind Ur is to serve as the ideal host for embedded domain-specific languages. For now, however, the ``generic'' functionality is intermixed with Ur/Web-specific functionality, including in these two library modules. We hope that these generic library components have types that speak for themselves. The next section introduces the Ur/Web-specific elements. Here, we only give the type declarations from the beginning of $\mathsf{Basis}$ .

$$\begin{array}{l} \mathsf{type} \; \mathsf{int} \\ \mathsf{... ...f} \; \mathsf{t} \times \mathsf{list} \; \mathsf{t} \end{array}$$

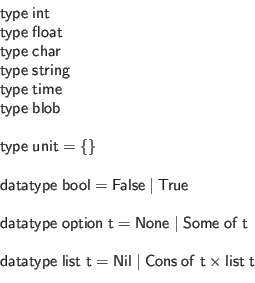
The only unusual element of this list is the $\mathsf{blob}$ type, which stands for binary sequences. Simple blobs can be created from strings via $\mathsf{Basis.textBlob}$ . Blobs will also be generated from HTTP file uploads.

Ur also supports polymorphic variants, a dual to extensible records that has been popularized by OCaml. A type $\mathsf{variant} \; r$ represents an $n$ -ary sum type, with one constructor for each field of record $r$ . Each constructor $c$ takes an argument of type $r.c$ ; the type $\{\}$ can be used to ``simulate'' a nullary constructor. The make function builds a variant value, while match implements pattern-matching, with match cases represented as records of functions.

$$\begin{array}{l} \mathsf{con} \; \mathsf{variant} :: \{\math... ...{t'} \to \mathsf{t}) \; \mathsf{ts}) \to \mathsf{t} \end{array}$$

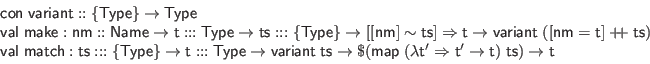
Another important generic Ur element comes at the beginning of top.urs.

$$\begin{array}{l} \mathsf{con} \; \mathsf{folder} :: \mathsf{... ...folder} \; \mathsf{r} \to \mathsf{tf} \; \mathsf{r} \end{array}$$

For a type-level record $\mathsf{r}$ , a $\mathsf{folder} \; \mathsf{r}$ encodes a permutation of $\mathsf{r}$ 's elements. The $\mathsf{fold}$ function can be called on a $\mathsf{folder}$ to iterate over the elements of $\mathsf{r}$ in that order. $\mathsf{fold}$ is parameterized on a type-level function to be used to calculate the type of each intermediate result of folding. After processing a subset $\mathsf{r'}$ of $\mathsf{r}$ 's entries, the type of the accumulator should be $\mathsf{tf} \; \mathsf{r'}$ . The next two expression arguments to $\mathsf{fold}$ are the usual step function and initial accumulator, familiar from fold functions over lists. The final two arguments are the record to fold over and a $\mathsf{folder}$ for it.

The Ur compiler treats $\mathsf{folder}$ like a constructor class, using built-in rules to infer $\mathsf{folder}$ s for records with known structure. The order in which field names are mentioned in source code is used as a hint about the permutation that the programmer would like.