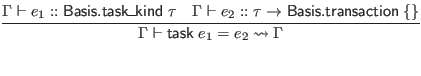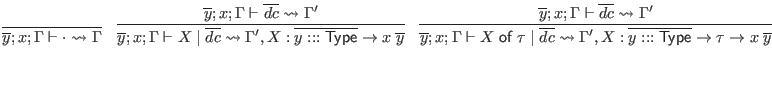We use an auxiliary judgment
![]() , expressing the enrichment of
, expressing the enrichment of ![]() with the types of the datatype constructors
with the types of the datatype constructors
![]() , when they are known to belong to datatype
, when they are known to belong to datatype ![]() with type parameters
with type parameters
![]() .
.
We presuppose the existence of a function
![]() , where
, where
![]() implements the
implements the
![]() declaration by producing a context with the appropriate entry for each available component of module
declaration by producing a context with the appropriate entry for each available component of module ![]() with signature items
with signature items
![]() . Where possible,
. Where possible,
![]() uses ``transparent'' entries (e.g., an abstract type
uses ``transparent'' entries (e.g., an abstract type ![]() is mapped to
is mapped to
![]() ), so that the relationship with
), so that the relationship with ![]() is maintained. A related function
is maintained. A related function
![]() builds a context containing the disjointness constraints found in
builds a context containing the disjointness constraints found in
![]() .
We write
.
We write
![]() as a shorthand, where
as a shorthand, where
![]() and
and
![]() . We write
. We write
![]() for the length of vector
for the length of vector
![]() of variables.
of variables.
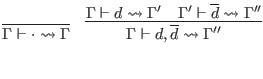
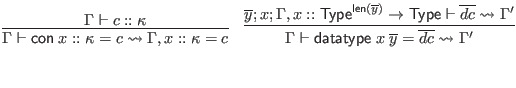
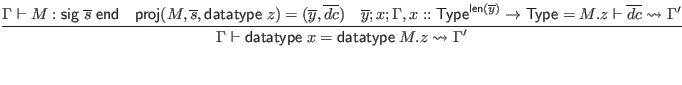
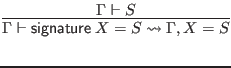
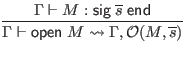
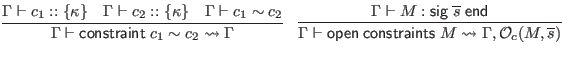
![$\displaystyle \infer{\Gamma \vdash \mathsf{table} \; x : c \leadsto \Gamma, x :...
...uery} \; [] \; [] \; (\mathsf{map} \; (\lambda \_ \Rightarrow []) \; c') \; c
}$](img235.png)