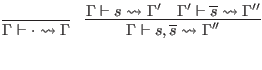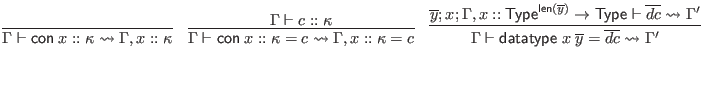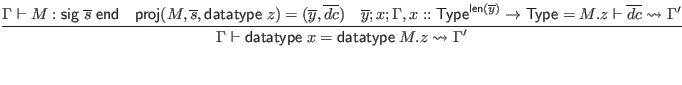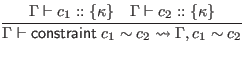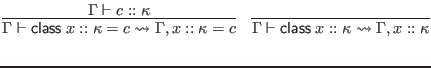We appeal to a signature item analogue of the
![]() function from the last subsection.
function from the last subsection.
This is the first judgment where we deal with constructor classes, for the
![]() forms. We will omit their special handling in this formal specification. Section 6.3 gives an informal description of how constructor classes influence type inference.
forms. We will omit their special handling in this formal specification. Section 6.3 gives an informal description of how constructor classes influence type inference.