


Next: Module Projection
Up: Static Semantics
Previous: Signature Compatibility
Contents
We use a helper function
 , which converts declarations and sequences of declarations into their principal signature items and sequences of signature items, respectively.
, which converts declarations and sequences of declarations into their principal signature items and sequences of signature items, respectively.



Next: Module Projection
Up: Static Semantics
Previous: Signature Compatibility
Contents
2014-07-14
![]() , which converts declarations and sequences of declarations into their principal signature items and sequences of signature items, respectively.
, which converts declarations and sequences of declarations into their principal signature items and sequences of signature items, respectively.
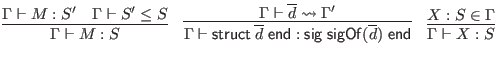
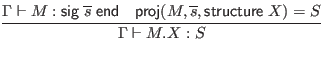
![$\displaystyle \infer{\Gamma \vdash M_1(M_2) : [X \mapsto M_2]S_2}{
\Gamma \vda...
...ma \vdash S_1
& \Gamma, X : S_1 \vdash S_2
& \Gamma, X : S_1 \vdash M : S_2
}$](img271.png)