Signature Compatibility

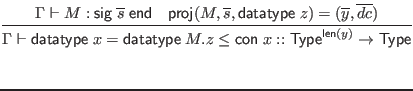
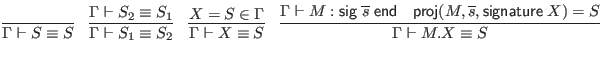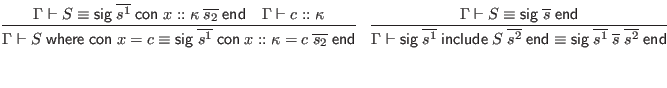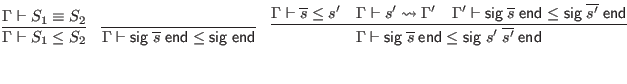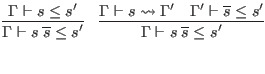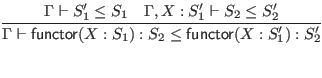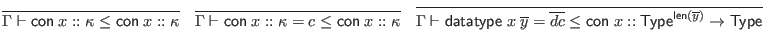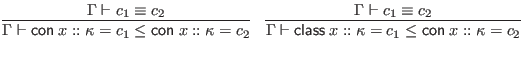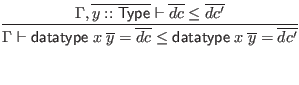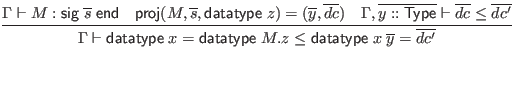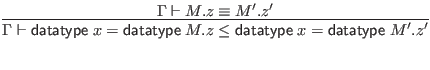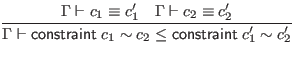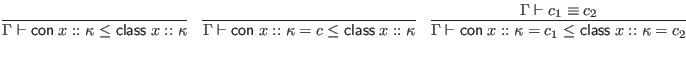To simplify the judgments in this section, we assume that all signatures are alpha-varied as necessary to avoid including multiple bindings for the same identifier. This is in addition to the usual alpha-variation of locally bound variables.

We rely on a judgment $\Gamma \vdash \overline{s} \leq s'$ , which expresses the occurrence in signature items $\overline{s}$ of an item compatible with $s'$ . We also use a judgment $\Gamma \vdash \overline{dc} \leq \overline{dc}$ , which expresses compatibility of datatype definitions.

$$\infer{\Gamma \vdash S \equiv S}{} \quad \infer{\Gamma \vdash S_1... ...; \mathsf{end} & \mathsf{proj}(M, \overline{s}, \mathsf{signature} \; X) = S }$$

$$\infer{\Gamma \vdash S \; \mathsf{where} \; \mathsf{con} \; x = c... ...f{end}}{ \Gamma \vdash S \equiv \mathsf{sig} \; \overline{s} \; \mathsf{end} }$$

$$\infer{\Gamma \vdash S_1 \leq S_2}{ \Gamma \vdash S_1 \equiv S_2... ...verline{s} \; \mathsf{end} \leq \mathsf{sig} \; \overline{s'} \; \mathsf{end} }$$

$$\infer{\Gamma \vdash s \; \overline{s} \leq s'}{ \Gamma \vdash s... ...s'}{ \Gamma \vdash s \leadsto \Gamma' & \Gamma' \vdash \overline{s} \leq s' }$$

$$\infer{\Gamma \vdash \mathsf{functor} (X : S_1) : S_2 \leq \maths... ... S'_2}{ \Gamma \vdash S'_1 \leq S_1 & \Gamma, X : S'_1 \vdash S_2 \leq S'_2 }$$

$$\infer{\Gamma \vdash \mathsf{con} \; x :: \kappa \leq \mathsf{con... ...hsf{con} \; x :: \mathsf{Type}^{\mathsf{len}(\overline y)} \to \mathsf{Type}}{}$$

$$\infer{\Gamma \vdash \mathsf{datatype} \; x = \mathsf{datatype} \... ...roj}(M, \overline{s}, \mathsf{datatype} \; z) = (\overline{y}, \overline{dc}) }$$

$$\infer{\Gamma \vdash \mathsf{class} \; x :: \kappa \leq \mathsf{c... ...ma \vdash \mathsf{class} \; x :: \kappa = c \leq \mathsf{con} \; x :: \kappa}{}$$

$$\infer{\Gamma \vdash \mathsf{con} \; x :: \kappa = c_1 \leq \math... ... = c_1 \leq \mathsf{con} \; x :: \kappa = c_2}{ \Gamma \vdash c_1 \equiv c_2 }$$

$$\infer{\Gamma \vdash \mathsf{datatype} \; x \; \overline{y} = \ov... ...Gamma, \overline{y :: \mathsf{Type}} \vdash \overline{dc} \leq \overline{dc'} }$$

$$\infer{\Gamma \vdash \mathsf{datatype} \; x = \mathsf{datatype} \... ...Gamma, \overline{y :: \mathsf{Type}} \vdash \overline{dc} \leq \overline{dc'} }$$

$$\infer{\Gamma \vdash \cdot \leq \cdot}{} \quad \infer{\Gamma \vda... ...vdash \tau_1 \equiv \tau_2 & \Gamma \vdash \overline{dc} \leq \overline{dc'} }$$

$$\infer{\Gamma \vdash \mathsf{datatype} \; x = \mathsf{datatype} \... ...datatype} \; x = \mathsf{datatype} \; M'.z'}{ \Gamma \vdash M.z \equiv M'.z' }$$

$$\infer{\Gamma \vdash \mathsf{val} \; x : \tau_1 \leq \mathsf{val}... ...ature} \; X = S_2}{ \Gamma \vdash S_1 \leq S_2 & \Gamma \vdash S_2 \leq S_1 }$$

$$\infer{\Gamma \vdash \mathsf{constraint} \; c_1 \sim c_2 \leq \ma... ...1 \sim c'_2}{ \Gamma \vdash c_1 \equiv c'_1 & \Gamma \vdash c_2 \equiv c'_2 }$$

$$\infer{\Gamma \vdash \mathsf{class} \; x :: \kappa \leq \mathsf{c... ... c_1 \leq \mathsf{class} \; x :: \kappa = c_2}{ \Gamma \vdash c_1 \equiv c_2 }$$

$$\infer{\Gamma \vdash \mathsf{con} \; x :: \kappa \leq \mathsf{cla... ... c_1 \leq \mathsf{class} \; x :: \kappa = c_2}{ \Gamma \vdash c_1 \equiv c_2 }$$